Klein four-group
| Group theory |
|---|
| Group theory |
|
Cyclic group Zn
Symmetric group, Sn Dihedral group, Dn Alternating group An Mathieu groups M11, M12, M22, M23, M24 Conway groups Co1, Co2, Co3 Janko groups J1, J2, J3, J4 Fischer groups F22, F23, F24 Baby Monster group B Monster group M |
|
|
|
Solenoid (mathematics)
Circle group General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) Lorentz group Poincaré group Conformal group Diffeomorphism group Loop group Infinite-dimensional Lie groups O(∞) SU(∞) Sp(∞) |
In mathematics, the Klein four-group (or just Klein group or Vierergruppe (English: four-group), often symbolized by the letter V) is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2. It was named Vierergruppe by Felix Klein in his Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade in 1884.
The Klein four-group is the smallest non-cyclic group. The only other group with four elements, up to isomorphism, is Z4, the cyclic group of order four (see also the list of small groups).
All non-identity elements of the Klein group have order 2. It is abelian, and isomorphic to the dihedral group of order (cardinality) 4. It is also isomorphic to the direct sum :
The Klein group's Cayley table is given by:
-
-
* 1 a b ab 1 1 a b ab a a 1 ab b b b ab 1 a ab ab b a 1
-
An elementary construction of the Klein four-group is the multiplicative group { 1, 3, 5, 7 } with the action being multiplication modulo 8. Here a is 3, b is 5, and ab is 3×5=15≡7 (mod 8).
In 2D it is the symmetry group of a rhombus and of a rectangle which are not squares, the four elements being the identity, the vertical reflection, the horizontal reflection, and a 180 degree rotation.
In 3D there are three different symmetry groups which are algebraically the Klein four-group V:
- one with three perpendicular 2-fold rotation axes: D2
- one with a 2-fold rotation axis, and a perpendicular plane of reflection: C2h = D1d
- one with a 2-fold rotation axis in a plane of reflection (and hence also in a perpendicular plane of reflection): C2v = D1h
The three elements of order 2 in the Klein four-group are interchangeable: the automorphism group is the group of permutations of the three elements. This essential symmetry can also be seen by its permutation representation on 4 points:
- V = { identity, (1,2)(3,4), (1,3)(2,4), (1,4)(2,3) }
In this representation, V is a normal subgroup of the alternating group A4 (and also the symmetric group S4) on 4 letters. In fact, it is the kernel of a surjective map from S4 to S3. According to Galois theory, the existence of the Klein four-group (and in particular, this representation of it) explains the existence of the formula for calculating the roots of quartic equations in terms of radicals, as established by Lodovico Ferrari: the map 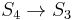 corresponds to the resolvent cubic, in terms of Lagrange resolvents.
corresponds to the resolvent cubic, in terms of Lagrange resolvents.
The Klein four-group as a subgroup of A4 is not the automorphism group of any simple graph. It is, however, the automorphism group of a two-vertex graph where the vertices are connected to each other with two edges, making the graph non-simple. It is also the automorphism group of the following simple graph, but in the permutation representation { (), (1,2), (3,4), (1,2)(3,4) } where the points are labeled top-left, bottom-left, top-right, bottom-right:
The Klein four-group is the group of components of the group of units of the topological ring of split-complex numbers.
In the construction of finite rings, eight of the eleven rings with four elements have the Klein four-group as their additive substructure.
The basic group of permutations in the twelve-tone technique is a four-group (Babbitt 1960, 253):
| S | I: | R: | RI: |
| I: | S | RI | R |
| R: | RI | S | I |
| RI: | R | I | S |
See also
References
- Milton Babbitt. "Twelve-Tone Invariants as Compositional Determinants", The Musical Quarterly, Vol. 46, No. 2, Special Issue: Problems of Modern Music. The Princeton Seminar in Advanced Musical Studies (Apr., 1960), pp. 246-259. Oxford University Press.
Further reading
- M.A. Armstrong (1988) Groups and Symmetry, Springer Verlag, page 53.
- W.E. Barnes (1963) Introduction to Abstract Algebra, D.C. Heath & Co., page 20.
- Weisstein, Eric W., "Klein Four-group" from MathWorld.